Hidden Markov models
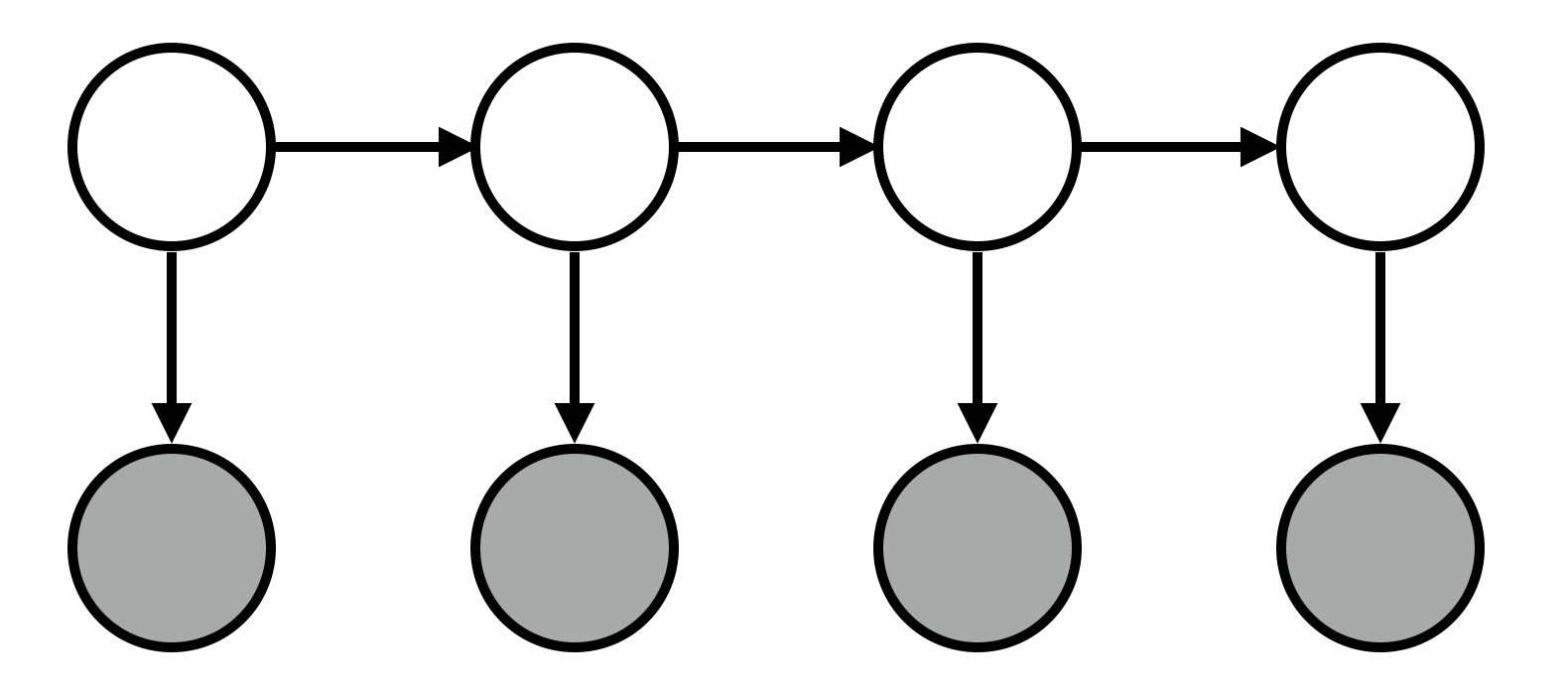
Markov models allow us to make predictions about elements in a sequence. Hidden Markov models (HMMs) generalize Markov models by positing that each of these elements has some hidden attributes, which we should be able to reason about. For instance, people typically perform actions for a reason (e.g., John went to get a drink with friends because he was happy). Typically, as observers, we see these actions but not their underlying causes; HMMs allow us to make inferences about them.
Sampling from an HMM
var states = "happy sad".split(" ");
var activities = "work commute exercise drink date sleep eat facebook".split(" ");
// transition matrix
var T = {
// current probability of next state:
// state happy sad
happy: [0.7, 0.3],
sad: [0.3, 0.7]
};
// emission matrix
var E = {
// probability of activity for state:
// stat work commute exercise drink date sleep eat facebook
happy: [9/24, 1/24, 1/24, 1/24, 1/24, 8/24, 2/24, 1/24],
sad: [2/24, 1/24, 0/24, 4/24, 0/24, 10/24, 2/24, 5/24]
// this isn't autobiographical! who said that?!
};
// given a state, sample the next state
var transition = function(state) {
var probs = T[state];
var sampledIndex = discrete(probs)
return states[sampledIndex];
}
// given a state, sample a corresponding activity
var emit = function(state) {
var probs = E[state];
var sampledIndex = discrete(probs)
return activities[sampledIndex]
}
var _sampleSequence = function(n, sequenceSoFar) {
if (n == 0) {
return sequenceSoFar
}
var prevState = _.last(sequenceSoFar).state
var nextState = transition(prevState)
var nextActivity = emit(nextState)
return _sampleSequence(n - 1,
sequenceSoFar.concat({state: nextState,
activity: nextActivity}));
}
// wrapper around _sampleSequence
var sampleSequence = function(n) {
// get the chain started by using a random seed state
// , which is 70% likely to be happy
var seedState = {state: flip(0.5) ? "happy" : "sad"};
return _sampleSequence(n, [seedState]).slice(1) // remove seed state;
}
var arrayEqual = function(x, y) {
return _.all(map(function(pair) { return pair[0] == pair[1] },
_.zip(x,y)))
}
Predicting activities from states:
print(Enumerate(function() {
var seq = sampleSequence(3);
var states = _.pluck(seq, "state");
var activities = _.pluck(seq, "activity");
factor( arrayEqual(states,
["happy", "happy", "happy"]
// ["sad", "sad", "sad"]
) ? 0 : -Infinity)
return activities.join(" ")
}, 100))
But we didn’t really need probabilistic programming for this… Let’s try the reverse question, which does require probabilistic programming: predicting states from activities.
print(Enumerate(function() {
var seq = sampleSequence(3);
var states = _.pluck(seq, "state");
var activities = _.pluck(seq, "activity");
factor( arrayEqual(activities,
["facebook", "facebook","facebook"]
//["commute","commute","commute"]
//["drink","exercise","date"]
) ? 0 : -Infinity)
return states.join(" ")
}))
Shortcoming of model: activities can influence states (e.g., exercising, drinking). Could address easily with PPL.
Application: part-of-speech tagging
var states = "_start noun verb det adj".split(" ");
var M = states.length;
var vocab = "saw walked dog man fort old the a boats".split(" ");
var N = vocab.length;
var grammar = [
["noun", "dog man fort old saw boats".split(" ")],
["det", "the a".split(" ")],
["verb","man saw walked".split(" ")],
["adj","old".split(" ")]
];
var E_fixed = _.object(
map(function(entry) {
var category = entry[0];
var members = entry[1];
var memberNumbers = map(function(x) { return vocab.indexOf(x) }, members);
var rangeN = _.range(N);
return [category,
map(function(n) { return memberNumbers.indexOf(n) > -1 ? 1 : 0 },
rangeN)];
},
grammar));
var stateParams = repeat(M - 1, function() { return 0.3 });
var vocabParams = repeat(N, function() { return 1 });
var pluck = function(xs, property) {
return map(function(x) { return x[property]},
xs
);
}
var model = function() {
// transition matrix represented as dictionary
// a key is a state; its corresponding value
// is an array of transition probabilities to states
var T = _.object(map(
function(s) {
// prevent transitions to ^
return [s, [0].concat(dirichlet(stateParams))];
},
states));
// emission matrix represented as dictionary
// a key is a state; its corresponding value
// is an array of transition probabilities to states
var E = E_fixed;
// var E = _.object(map(
// function(s) {
// return [s, dirichlet(vocabParams)];
// },
// states));
// given a current state, sample the next state
var transition = function(state) {
var probs = T[state];
return states[discrete( probs )];
}
// given a current state, emit a word for that state
var emit = function(state) {
var probs = E[state];
return vocab[discrete( probs )];
}
var _observePairs = function(pairsLeft, pairsSoFar) {
if (pairsLeft.length == 0) {
return pairsSoFar;
}
var prevPair = pairsSoFar[pairsSoFar.length - 1];
var prevState = prevPair.state;
var nextState = pairsLeft[0].state;
var sampledNextState = transition(prevPair.state);
factor(nextState == "?" ? 0 :
(sampledNextState == nextState ? 0 : -30));
var nextWord = pairsLeft[0].word;
var sampledNextWord = emit(sampledNextState);
factor(sampledNextWord == nextWord ? 0 : -10);
return _observePairs(pairsLeft.slice(1), pairsSoFar.concat({state: sampledNextState,
word: sampledNextWord
}));
}
var observePairs = function(words, states) {
// zip together states and words into
// [[state1,word1], [state2, word2], ..., [statek, wordk]]
// and then convert each array to a {state: ..., word: ...} object
var zipped = _.zip(words.split(/ +/),
states.split(/ +/));
var objectify = function(x) {
return {
word: x[0],
state: x[1]
}
}
var pairs = map(objectify, zipped);
return _observePairs(pairs,
[{state: "_start", word: ""}]).slice(1);
}
repeat(20,
function() {
observePairs("the man",
"det noun")
observePairs("the old dog",
"det adj noun")
observePairs("the man walked a dog",
"det noun verb det noun")
observePairs("a dog saw the fort",
"det noun verb det noun")
observePairs("man the fort",
"verb det noun")
observePairs("man the boats",
"verb det noun")
observePairs("a man walked",
"det noun verb")
observePairs("dog saw the boats",
"noun verb det noun")
})
var x = observePairs( "the old man the fort",
"? ? ? ? ?");
//"det noun verb det noun");
return pluck(x, "state");
};
print(ParticleFilter(model, 1000));